Ambrus Kaposi
Teaching
Advertisements
Drafts and publications
Talks
Floorplans
Other
Associate professor
Department of Programming Languages and Compilers
Faculty of Informatics
Eötvös Loránd University
Pázmány Péter sétány 1/C
1117 Budapest
Hungary
Room: 2-620 in the South Building
(location
of building, floorplans of building). If the door in the corridor is locked, you can use
the interphone next to the door to call my room.
Email: akaposi@inf.elte.hu
Office hours (fogadóóra): Tuesday 15.00-16.00
Office phone: +36 1 3722500 / 8497
Teaching
Teaching in 2024 Autumn semester at Eötvös Loránd University:
Older teaching materials:
Advertisements
Budapest
type theory seminar once a week, very informal, everyone is
welcome to join.
If you are interested in functional programming or type theory, the
best way to learn and get involved is to go to one of the following
excellent (summer) schools. Usually they have scholarships for student
attendees.
If you want to do a research project (TDK), dissertation
(diplomamunka), or PhD in type theory, please contact
me. Here are some random topics and keywords, but
you can also bring your own topic. Also look at the "further work"
sections in the papers below and in the topics
of type theory
seminars.
- metatheory of type theory, e.g. normalisation, parametricity,
univalence, gluing, definability, classical principles, equivalent
algebraic definitions of type theory
- classes of (co)inductive types and translations between them,
e.g. W-types, indexed W-types, quotients, IITs, QIITs, HIITs,
M-types
- formalisation in Agda/Coq, e.g. Fóthizmus, discrete math, type
systems, formal semantics
- programming with dependent types, e.g. interactive programs
using this
- type checker, interpreter, compiler for a programming language
with dependent types,
see here
- Runtime reflection
- develop FUSE filesystems for: showing syntax tree from a file,
showing emails through IMAP, indexing, search by creating a folder
- medical application: develop an easy-to use online interface
for this
- medical application: develop a plugin
for FlowJo performing the same
analysis
as Facskin or
improve Facskin
Drafts and publications
All comments are very much welcome. Other lists: MTMT, dblp, Google Scholar. Some bibtex items.
- Type theory in type theory with single substitutions
- with Szumi Xie
- Submitted to CPP 2025
- formalisation
- Second-order generalised algebraic theories: signatures and first-order semantics
- with Szumi Xie
- FSCD 2024
- implementation and detailed constructions
- Formális nyelv = másodrendű algebrai elmélet (Hungarian)
- Húszéves az ELTE Eötvös József Collegium Informatikai Műhelye, 2024
- A filozófia csodálatos hatékonysága a formális tudományokban (Hungarian)
- with Zoltán Molnár
- Érintő Elektronikus Matematikai Lapok, Sep 2023
- Internal parametricity, without an interval
- with Thorsten Altenkirch, Yorgo Chamoun and Michael Shulman
- POPL 2024
- For the metatheory of type theory, internal sconing is enough
- with Rafaël Bocquet and Christian Sattler
- FSCD 2023
- Slides by Rafaël
- Combinatory logic and lambda calculus are equal, algebraically
- with Thorsten Altenkirch, Artjoms Šinkarovs and Tamás Végh
- FSCD 2023
- formalisation
- The Münchhausen method in type theory
- with Thorsten Altenkirch, Artjoms Šinkarovs and Tamás Végh
- TYPES 2022 post-proceedings
- source code and formalisation
- Internal strict propositions using point-free equations
- with István Donkó
- TYPES 2021 post-proceedings
- formalisation
- Relative induction principles for type theories
- with Rafaël Bocquet and Christian Sattler
- Feb 2021
- A calculus of single substitutions for simple type theory
- with Norbert Luksa
- MACS 2020
- formalisation
- Constructing a universe for the setoid model
- with Thorsten Altenkirch, Simon Boulier, Christian Sattler, Filippo Sestini
- FoSSaCS 2021
- formalisation
- Large and Infinitary Quotient Inductive-Inductive Types
- with András Kovács
- LICS 2020
- For finitary induction-induction, induction is enough
- with András Kovács and Ambroise Lafont
- TYPES 2019 post-proceedings
- formalisation
- A Syntax for Mutual Inductive Families
- with Jakob von Raumer
- FSCD 2020
- formalisation
- Shallow Embedding of Type Theory is Morally Correct
- with András Kovács and Nicolai Kraus
- MPC 2019
- formalisation
- Gluing for type theory
- with Simon Huber and Christian Sattler
- FSCD 2019
- formalisation
- Setoid type theory — a syntactic translation
- with Thorsten Altenkirch, Simon Boulier and Nicolas Tabareau
- MPC 2019
- formalisation
- Signatures and Induction Principles for Higher Inductive-Inductive Types
- with András Kovács
- LMCS, 2020
- formalisation
- Constructing Quotient Inductive-Inductive Types
- with Thorsten Altenkirch and András Kovács
- POPL 2019
- appendix
- formalisation
- A syntax for higher inductive-inductive types
- with András Kovács
- FSCD 2018, received Best Paper Award for Junior Researcher
- formalisation
- Codes for quotient inductive-inductive types
- with András Kovács
- Draft, Oct 2017
- A fröccs szintaxisa és operációs szemantikája
- ELTE Fröccs Akadémia, 2017
- formalisation
- Normalisation by Evaluation for Type Theory, in Type Theory
- with Thorsten Altenkirch
- LMCS, 2017
- formalisation
- Type theory in a type theory with quotient inductive types
- PhD thesis (type theory), date of defence: 24 Nov 2016
- Advisor: Graham Hutton
- formalisation
- Normalisation by Evaluation for Dependent Types
- with Thorsten Altenkirch
- FSCD 2016
- formalisation
- Type Theory in Type Theory using Quotient Inductive Types
- with Thorsten Altenkirch
- POPL 2016
- formalisation
- Towards a cubical type theory without an interval
- with Thorsten Altenkirch
- TYPES 2015 post-proceedings
- Formalising the completeness theorem of classical propositional logic in Agda
- with Leran Cai and Thorsten Altenkirch
- Draft, Mar 2015
- Free Applicative Functors
- with Paolo Capriotti
- MSFP 2014
- comments
- Bevezetés a homotópia-típuselméletbe (Hungarian)
- Tízéves az ELTE Eötvös József Collegium Informatikai Műhelye, 2014
- First year report
- An introduction to type theory with a notation using De Bruijn
indices and explicit substitutions. Nov 2013.
- Kinetikus áramlási citometriás mérések értékelése
- PhD thesis (medicine), date of defence: 24 Jun 2013
- Advisor: Barna Vásárhelyi
- Analysis Software for FACS-measurements
- BSc dissertation (szakdolgozat). May 2012
Talks
- Internal relational parametricity, without an interval
- TYPES, Copenhagen, 11 June 2024
- abstract
- Internal parametricity, without an interval
- POPL, London, 19 Jan 2024
- video
- A type theory with internal parametricity
- World logic day, Pécs, 12 Jan 2024
- Abstract
- video
- Neumann János doktori disszertációja
- A gondolkodás architektúrái, Neumann 120 emlékév, ELTE, Budapest, 6 Sep 2023
- video
- Combinatory logic and lambda calculus are equal, algebraically
- FSCD, Rome, 3 July 2023
- Towards quotient inductive-inductive-recursive types
- TYPES, Valencia, 13 June 2023
- video
- abstract
- formalisation
- Neumann János doktori disszertációja
- Neumann Nap, ELTE Informatikai Kar, Budapest, 11 May 2023
- video
- Why is equality interesting? (Second order generalised algebraic theories)
- World logic day, Rényi Institute, Budapest, 13 Jan 2023
- Type Theory in Type Theory using Quotient-Inductive-Inductive-Recursive Types
- Types, Thorsten and Theories. A workshop on type theory in honour of Thorsten's 60th birthday, Nottingham and online, 12 Oct 2022
- abstract
- Towards Higher Observational Type Theory
- TYPES, Nantes, 20 Jun 2022
- abstract
- video
- A legegyszerűbb programozási nyelv
- Kutatók Éjszakája, Budapest, 24 Sep 2021
- Levels of abstraction when defining type theory in type theory
- Celebrating 90 Years of Gödel's Incompleteness Theorems, Nürtingen, 6 Jul 2021
- video
- Quotient inductive-inductive types in the setoid model
- TYPES, online (Leiden), 14 Jun 2021
- abstract
- Jobb programozási nyelvekkel a megbízható szoftverekért
- 3in projekt zárórendezvény, online, 26 Nov 2020
- Quotient inductive-inductive types and higher friends
- HoTTEST, online, 22 Oct 2020
- video
- Shallow embedding of type theory is morally correct
- MPC, Porto, 8 Oct 2019
- Quotient inductive-inductive types
- STCS, Szombathely, 22 Feb 2019
- Algebraic programming language theory
- PLC Department Workshop, Bugyi, 11 Jan 2019
- Induction-induction Part 3
- TYPES, Braga, 21 Jun 2018
- abstract
- Specifying higher inductive-inductive types
- Université de Nantes, 25 Apr 2018
- A syntax for higher inductive-inductive types
- Agda Implementors' Meeting, Budapest, 31 Jan 2018
- A syntax for higher inductive-inductive types
- EUTypes Working Meeting, Nijmegen, 23 Jan 2018
- Bizonyítás és programozás
- Pannonhalmi Bencés Gimnázium, 24 Nov 2017
- Normalisation by Evaluation for a Type Theory with Large Elimination
- TYPES, Budapest, 30 May 2017
- abstract
- Formalising the metatheory of type theory using quotient inductive types
- FPFM, Nantes, 27 Apr 2017
- Normalisation by evaluation for an intrinsic syntax of type theory
- EUTypes Meeting, Ljubljana, 31 Jan 2017
- Normalisation by Evaluation for Dependent Types
- FSCD, Porto, 24 Jun 2016
- Normalisation by Evaluation for Dependent Types
- TYPES, Novi Sad, 25 May 2016
- abstract
- Type theory in type theory using quotient inductive types
- Theoretical computer science seminar, University of Birmingham, 26 Feb 2016
- Type Theory in Type Theory using Quotient Inductive Types
- POPL, St Petersburg, Florida, 20 Jan 2016
- poster
- video
- A nominal syntax for internal parametricity
- TYPES, Tallinn, 21 May 2015
- abstract
- Bevezetés a homotópia-típuselméletbe
- Eötvös Kollégium, Budapest, 7 Jan 2015
- Bizonyítás és programozás
- Hackerspace, Budapest, 6 Jan 2015
- A syntax for cubical type theory
- with Thorsten Altenkirch
- HoTT Workshop, Oxford, 8 Nov 2014
- video
- A syntax for cubical type theory
- University of Bath, 4 Nov 2014
- A syntax for cubical type theory
- AIM XIX, Paris, 23 May 2014
- Bevezetés a homotópia-típuselméletbe
- Tízéves az ELTE Eötvös József Collegium Informatikai Műhelye Konferencia, Budapest, 21 Feb 2014
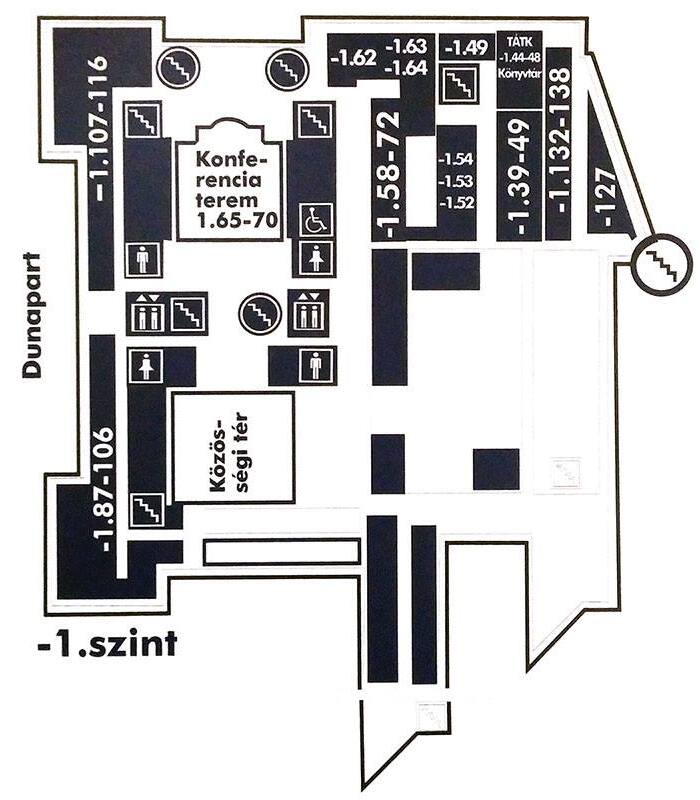
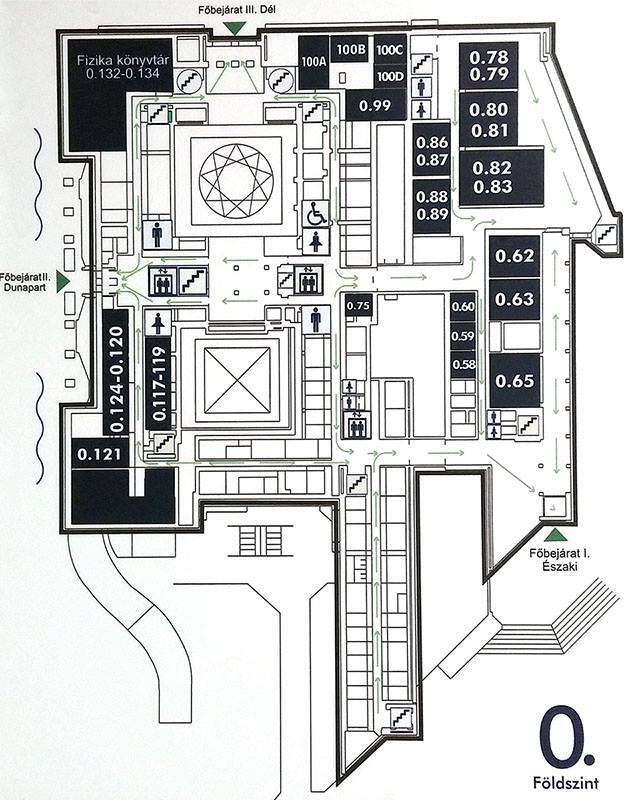
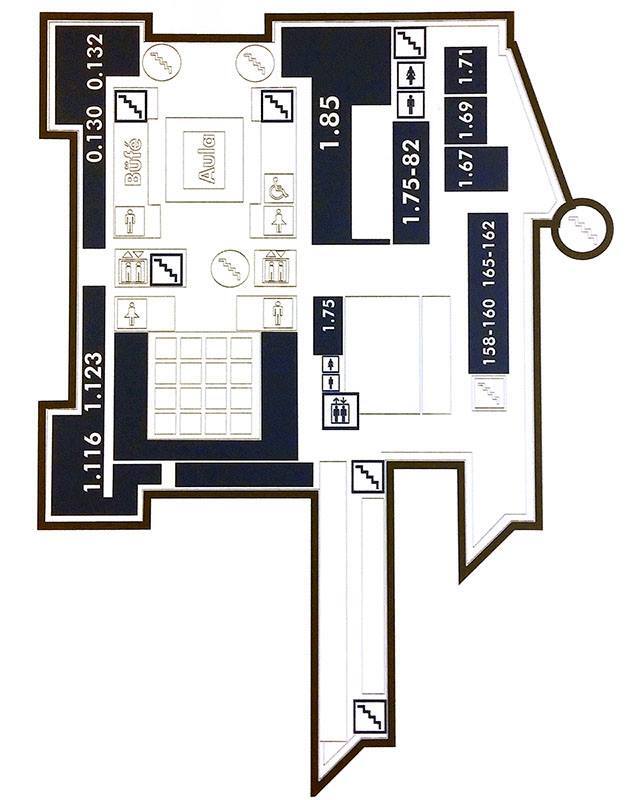
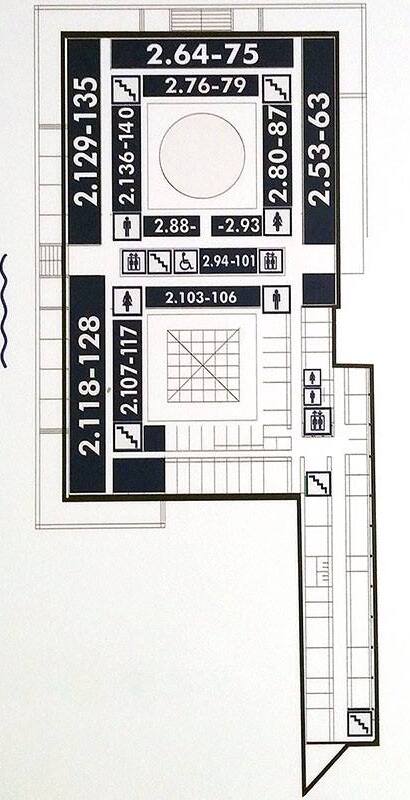
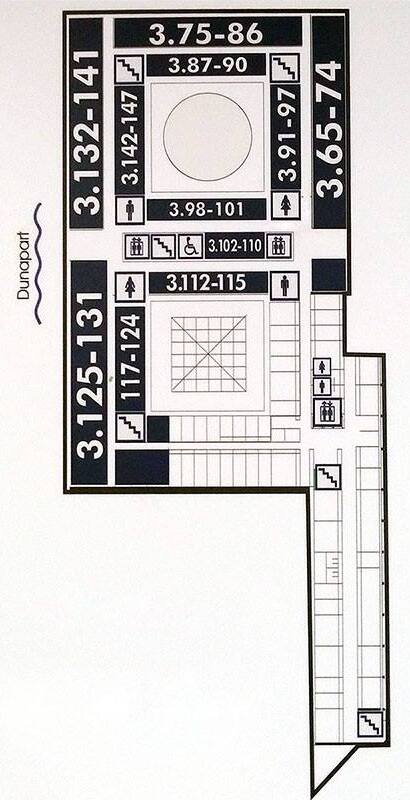
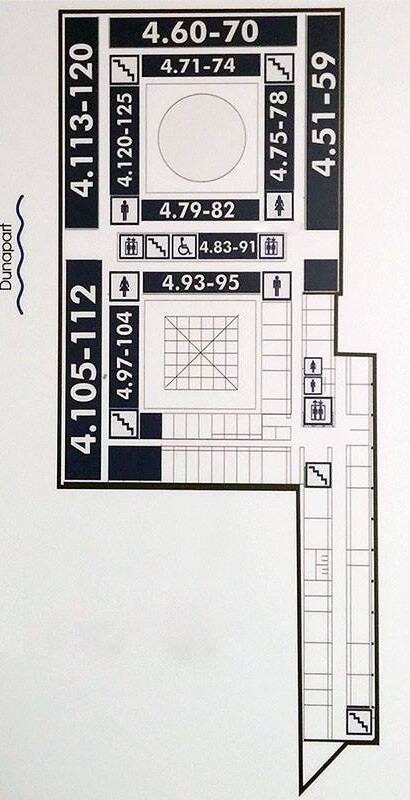
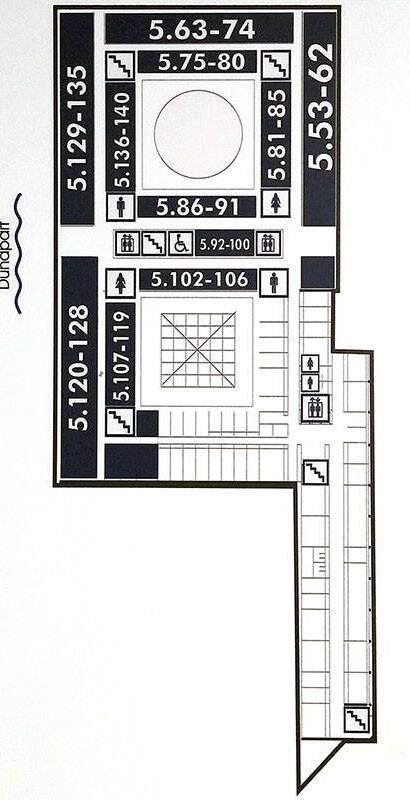
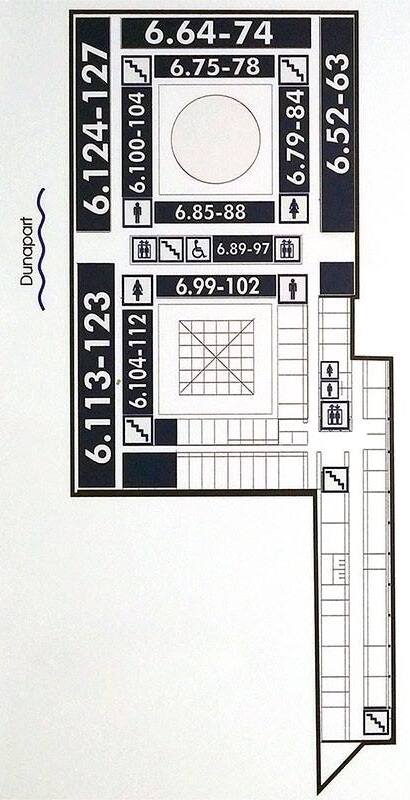
Floorplans of ELTE Lágymányos buildings
3D maps of all ELTE buildings in Budapest. The source of the maps below is Gabeee's page, I fixed some errors.
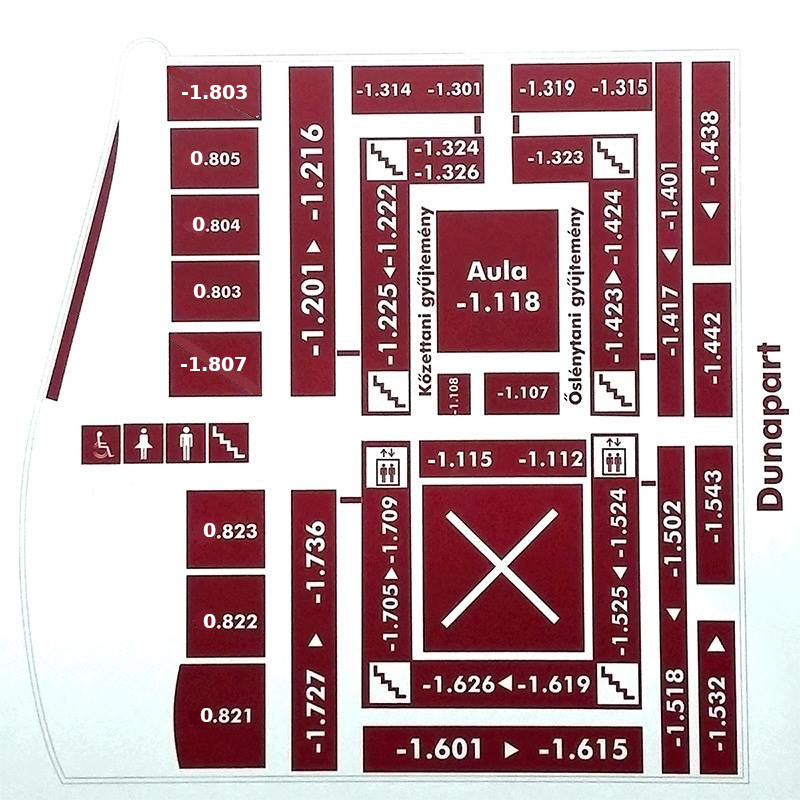
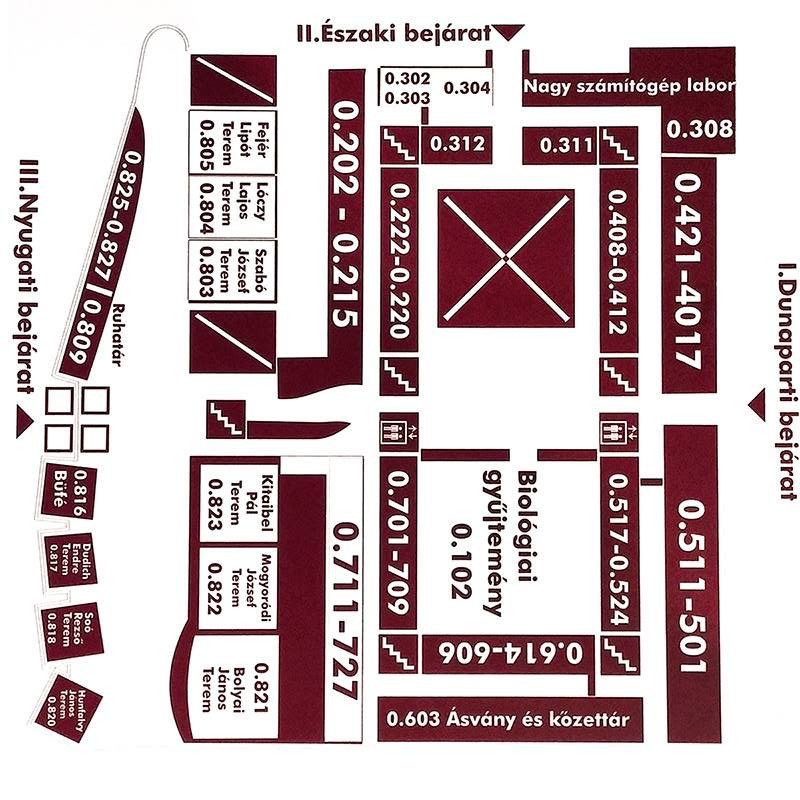
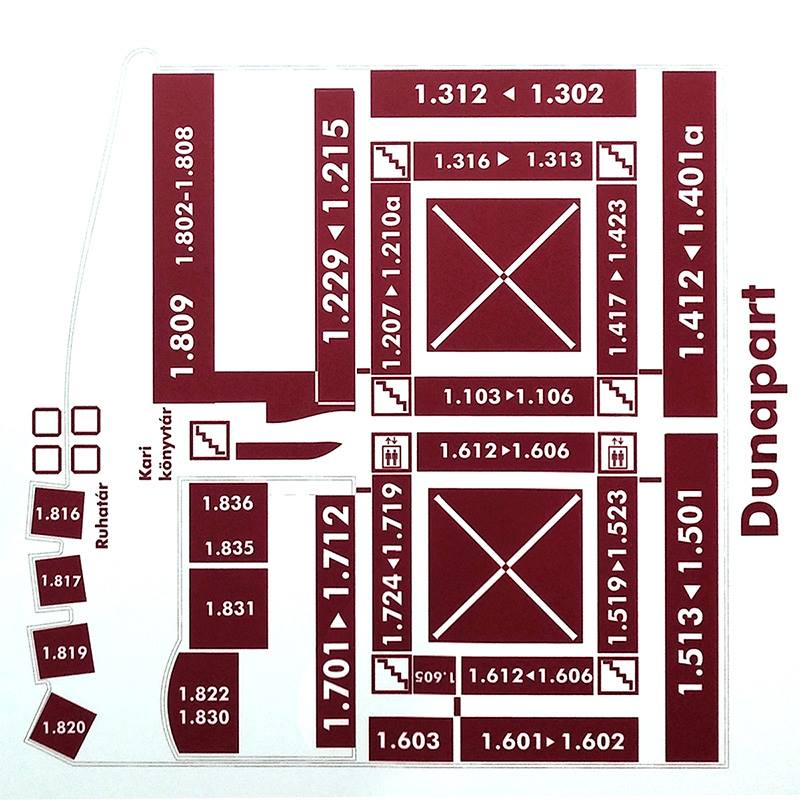
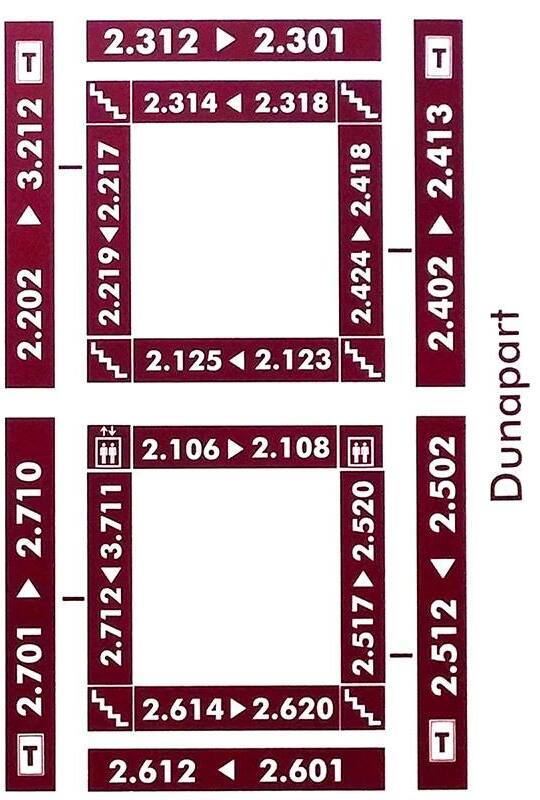
South building
Address: Pázmány Péter sétány 1/C 1117 Budapest Hungary. Floors -1 (also called 00), 0,1,2,3,4,5,6,7. North is upwards.
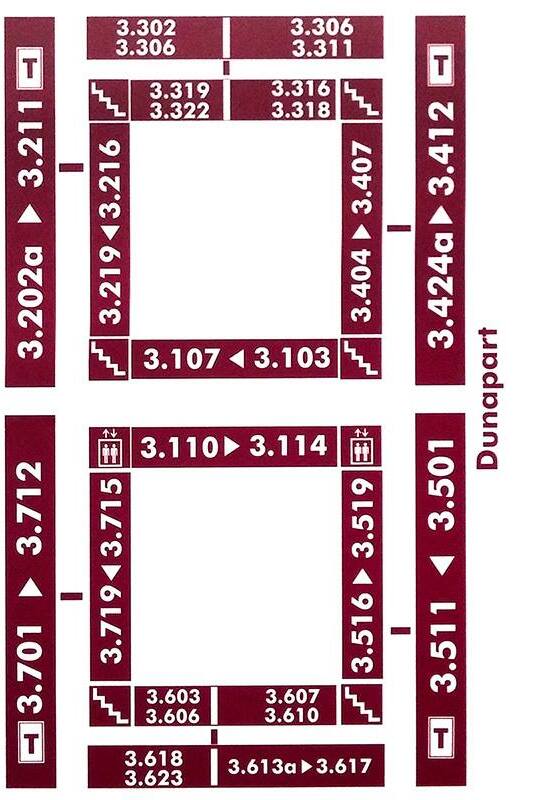
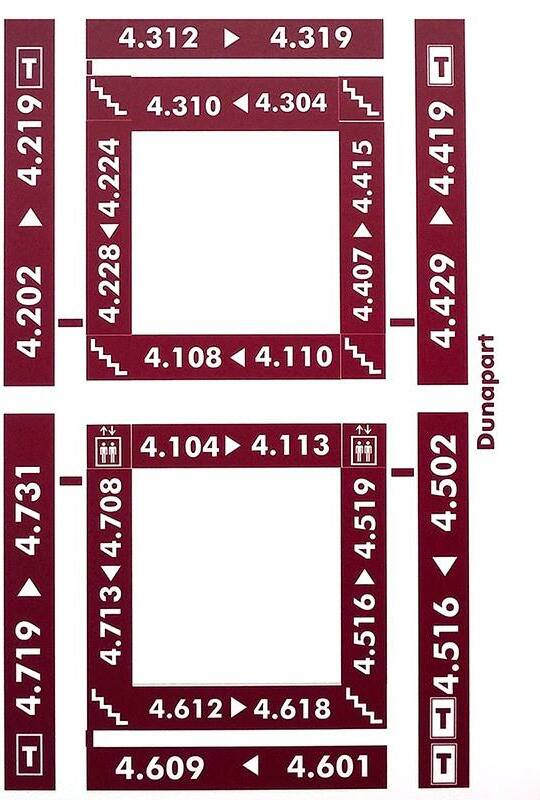
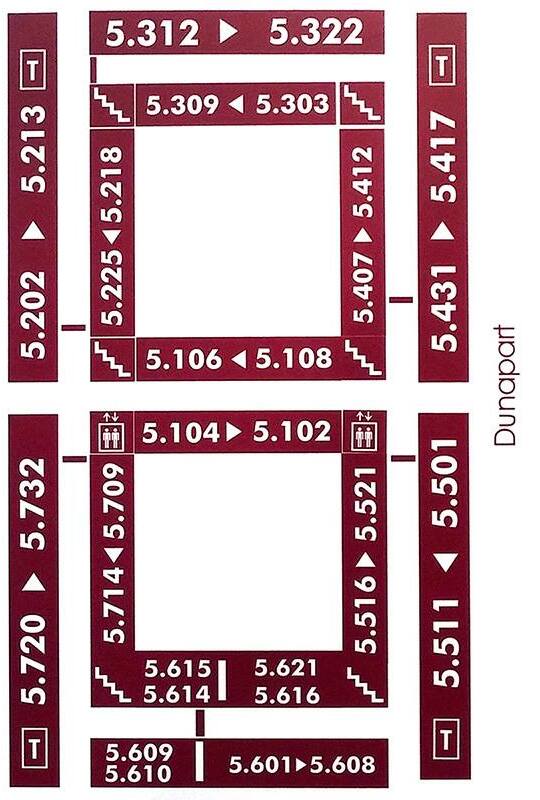
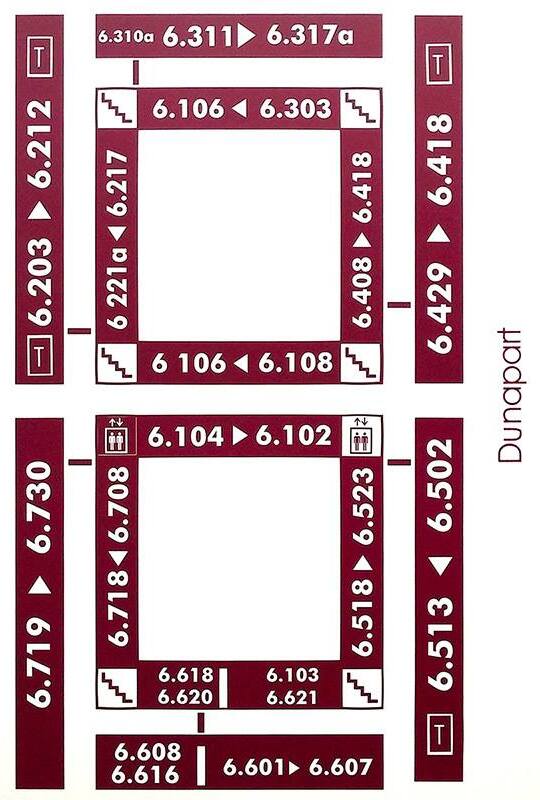
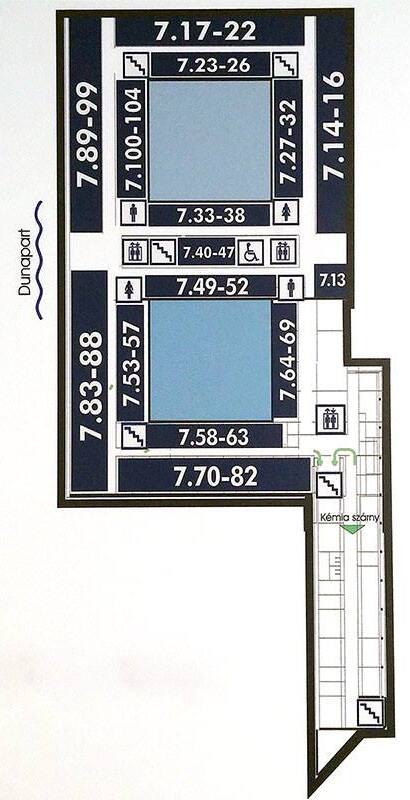
North building
Address: Pázmány Péter sétány 1/A 1117 Budapest Hungary. Floors -1, 0,1,2,3,4,5,6,7. North is downwards.
Other
Nottingham FP Lab Away Day 2013