Tisztaság (mellékhatás-mentesség) (2/2)
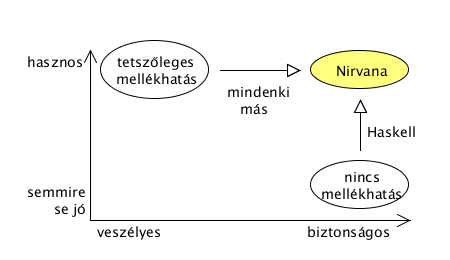
Nirvana elérése
Simon-Peyton Jones ábrája innen
Java:
osszeg = 0;
for (int i = 1; i <= 10; ++i)
osszeg = osszeg + i;Haskell:
sum [1..10]Példák:
f [] = []
f (x:xs) = f as ++ [x] ++ f bs
where
as = [a | a <- xs, a <= x]
bs = [b | b <- xs, x < b]f [] = []
f (x:xs) = f as ++ [x] ++ f bs
where
as = [a | a <- xs, a <= x]
bs = [b | b <- xs, x < b]Magyarázat:
f(x, y) helyett f x yf x + y jelentése f(x) + y (függvényalkalmazás kötési erőssége a legnagyobb)sqr x = x * x[]1 : []1 : (2 : (3 : []))[1, 2, 3][1..3][a | a <- [1..], a <= 3] jelentése { a : a ∈ ℕ, a ≤ 3}++, <=, <[1,2,3] ++ [3,4,5] eredménye [1,2,3,4,5]Függvényhívás Eredmény
-----------------------------------
head [1,2,3,4,5] 1
tail [1,2,3,4,5] [2,3,4,5]
[1,2,3,4,5] !! 2 3 (infix)
take 3 [1,2,3,4,5] [1,2,3]
drop 3 [1,2,3,4,5] [4,5]
length [1,2,3,4,5] 5
[1,2,3] ++ [4,5] [1,2,3,4,5] (infix)
reverse [1,2,3,4,5] [5,4,3,2,1]
sum [1,2,3,4,5] 15
product [1,2,3,4,5] 120Példák a használatukra:
factorial n = product [1..n]
average ns = sum ns `div` length nsFeladatok:
last definiálása a fentiekkel: lista utolsó elemeinit definiálása a fentiekkel: lista utolsó elemén kívül a többilast ns = head (reverse ns)
last ns = ns !! (length ns - 1)
init ns = take (length ns - 1) ns
init ns = reverse (tail (reverse ns))
(f . g) x = f (g x)
last = head . reverse
init = reverse . tail . reverseEz történik futási időben:
take :: Int -> [a] -> [a]
take n xs | n <= 0 = [] -- (A)
take n [] = [] -- (B)
take n (x:xs) = x : take (n - 1) xs -- (C)
take 3 (1:2:3:4:5:[]) -- [1,2,3,4,5]
~> (C)
1 : take 2 (2:3:4:5:[])
~> (C)
1 : 2 : take 1 (3:4:5:[])
~> (C)
1 : 2 : 3 : take 0 (4:5:[])
~> (A)
1 : 2 : 3 : [] -- [1,2,3]
take 3 (1:[]) -- [1]
~> (C)
1 : take 2 []
~> (B)
1 : [] -- [1]A Church-féle lambda-kalkulusban béta-redukciónak hívjuk.
statikus, polimorf típusokTrue :: Bool
False :: Bool
'a' :: Char
1 :: Integer
1.1 :: Double
> 1 + False
ERROR[False, True, False] :: [Bool]
[’a’,’b’,’c’,’d’] :: [Char]A hossz nem számít:
[False, True] :: [Bool]Tetszőleges típusú listák hozhatók létre:
[[’a’],[’b’,’c’]] :: [[Char]](False,True) :: (Bool,Bool)
(False,’a’,True) :: (Bool,Char,Bool)A hossz számít:
(False,True) :: (Bool,Bool)
(False,True,False) :: (Bool,Bool,Bool)Tetszőleges típusú n-esek hozhatók létre:
(’a’,(False,’b’)) :: (Char,(Bool,Char))
(True,[’a’,’b’]) :: (Bool,[Char])not :: Bool -> Bool
add :: (Int,Int) -> Int
add (a,b) = a + b
add' :: Int -> (Int -> Int)
add' a b = a + b
sum :: [Int] -> IntPolimorf típusok:
id :: a -> a
const :: a -> b -> a
head :: [a] -> a
length :: [a] -> Int
fst :: (a,b) -> aMagasabbrendű függvények:
map :: (a -> b) -> [a] -> [b]
filter :: (a -> Bool) -> [a] -> [a]member :: a -> [a] -> Bool
sort :: [a] -> [a]
show :: a -> String
(+) :: a -> a -> a
(*) :: a -> a -> a
(/) :: a -> a -> a
sqrt :: a -> amember :: a -> [a] -> Bool
member :: Eq a => a -> [a] -> Bool
class Eq a where
(==) :: a -> a -> Bool
instance Eq Bool where
True == True = True
False == False = True
_ == _ = False
sort :: [a] -> [a]
sort :: Ord a => [a] -> [a]
sqr :: a -> a
sqr :: Num a => a -> aEz volt a Haskell legnagyobb újdonsága a Mirandához, ML-hez képest.
tisztaMit csinálhatnak az alábbi függvények?
f :: a -> a
g :: [a] -> [a]
h :: [a] -> a
i :: (a,b) -> b
j :: a -> blustasqr (3+4) ~> (3+4) * (3+4) ~> 7 * 7 ~> 49
> ones = 1 : ones -- így is lehetne: ones = [1..]
> take 5 ones -- béta redukció
[1,1,1,1,1]
take 5 ones
\____/ \___/
| |
vezérlés adatAz alábbi számítás O(n) futási idejű:
min = head . sort -- típusa?min :: Ord a => [a] -> atake :: Int -> [a] -> [a]
take n xs | n <= 0 = [] -- (A)
take n [] = [] -- (B)
take n (x:xs) = x : take (n - 1) xs -- (C)
ones ::
ones = 1 : ones -- (D)
take 3 ones
~> (D) (szükség van rá, hogy az (A)-(B)-(C) esetszétválasztás megtörténhessen)
take 3 (1 : ones)
~> (C)
1 : take 2 ones
~> (D)
1 : take 2 (1 : ones)
~> (C)
1 : (1 : take 1 ones)
~> (D)
1 : (1 : take 1 (1 : ones))
~> (C)
1 : (1 : (1 : take 0 ones))
~> (A)
1 : (1 : (1 : []))Egy Haskell program emiatt:
min xs = head . sort $ xs O(n) futási idejű)f :: a -> a), könnyű tesztelni, érthetőbb a programtemplate <typename T>
void qsort (T *result, T *list, int n)
{
if (n == 0) return;
T *smallerList, *largerList;
smallerList = new T[n];
largerList = new T[n];
T pivot = list[0];
int numSmaller=0, numLarger=0;
for (int i = 1; i < n; i++)
if (list[i] < pivot)
smallerList[numSmaller++] = list[i];
else
largerList[numLarger++] = list[i];
qsort(smallerList,smallerList,numSmaller);
qsort(largerList,largerList,numLarger);
int pos = 0;
for ( int i = 0; i < numSmaller; i++)
result[pos++] = smallerList[i];
result[pos++] = pivot;
for ( int i = 0; i < numLarger; i++)
result[pos++] = largerList[i];
delete [] smallerList;
delete [] largerList;
};Magasabbrendű függvények:
numOf p xs = length (filter p xs)
numOfEven xs = numOf even xs
numOfGE5 xs = numOf (>=5) xsA tisztaság miatt nagyon egyszerűen párhuzamosítható:
qs :: [Float] -> [Float]
qs [] = []
qs (x:xs) = qs as ++ [x] ++ qs bs
where
as = [a | a <- xs, a <= x]
bs = [b | b <- xs, x < b]A tisztaság miatt nagyon egyszerűen párhuzamosítható:
qs :: [Float] -> [Float]
qs [] = []
qs (x:xs) = qs as ++ [x] ++ qs bs
where
as = [a | a <- xs, a <= x] `using` rpar
bs = [b | b <- xs, x < b] `using` rparEgyenlőségi érvelés (gimnázium: (x+a)*(x+b) = ... = x*x + x*b + a*x + a*b)
(++) :: [a] -> [a] -> [a]
[] ++ ys = ys -- (A)
(x:xs) ++ ys = x : (xs ++ ys) -- (B)Bal oldalt helyettesíthetjük mindig a jobb oldallal és fordítva.
A következőt szeretnénk bizonyítani:
as ++ (bs ++ cs) ≡ (as ++ bs) ++ csEgyenlőségi érvelés (gimnázium: (x+a)*(x+b) = ... = x*x + x*b + a*x + a*b)
(++) :: [a] -> [a] -> [a]
[] ++ ys = ys -- (A)
(x:xs) ++ ys = x : (xs ++ ys) -- (B)Bal oldalt helyettesíthetjük mindig a jobb oldallal és fordítva.
A következőt szeretnénk bizonyítani:
as ++ (bs ++ cs) ≡ (as ++ bs) ++ csTeljes indukció as mérete szerint. Alapeset:
[] ++ (bs ++ cs)
≡ (A)>
bs ++ cs
≡ <(A)
([] ++ bs) ++ csInduktív eset:
(a:as) ++ (bs ++ cs)
≡ (B)>
a : (as ++ (bs ++ cs))
≡ (indukciós feltevés)
a : ((as ++ bs) ++ cs)
≡ <(B)
((a : (as ++ bs)) ++ cs)
≡ <(B)
(((a:as) ++ bs) ++ cs)statikus, polimorf típusok (típusrendszer)Programok helyességének biztosítása:
| Módszer | Példa |
|---|---|
| tesztelés | Java JUnit framework |
| futásidejű monitorozás | Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException |
| modell-ellenőrzés | NuSMV |
state : {ready, busy}, request : boolean |
|
init(state) := ready |
|
next(state) := if state = ready & request = TRUE |
|
then busy else {ready, busy} |
|
| típusrendszerek | 4 :: Int |
[1,2,4] :: List Int |
|
(+) 4 :: Int -> Int |
|
(+) :: Num a => a -> a -> a |
|
| formális ellenőrzés | B módszer (metró), Hoare-logika, Isabelle, Coq |
Haskellben megadható a négyzetes mátrixok típusa (de bonyolult)
Az alábbi típusok már nem:
| Módszer | Példa |
|---|---|
| tesztelés | Java JUnit framework |
| futásidejű monitorozás | Exception in thread "main" java.lang.ArrayIndexOutOfBoundsException |
| modell-ellenőrzés | NuSMV |
state : {ready, busy}, request : boolean |
|
init(state) := ready |
|
next(state) := if state = ready & request = TRUE |
|
then busy else {ready, busy} |
|
| típusrendszerek | 4 :: Int |
[1,2,4] :: List Int |
|
(+) 4 :: Int -> Int |
|
(+) :: Num a => a -> a -> a |
|
| formális ellenőrzés | B módszer (metró), Hoare-logika, Isabelle, Coq |
Típusrendszert a formális ellenőrzés szintjéig erősítjük.
++-assoc :: (as bs cs :: List) -> as ++ (bs ++ cs) ≡ (as ++ bs) ++ cs
++-assoc [] bs cs = ≡-refl
++-assoc (a : as) bs cs = cong (a:) (++-assoc as bs cs)Emlékeztető:
Teljes indukció as mérete szerint. Alapeset:
[] ++ (bs ++ cs)
≡ (A)>
bs ++ cs
≡ <(A)
([] ++ bs) ++ csInduktív eset:
(a:as) ++ (bs ++ cs)
≡ (B)>
a : (as ++ (bs ++ cs))
≡ (indukciós feltevés)
a : ((as ++ bs) ++ cs)
≡ <(B)
((a : (as ++ bs)) ++ cs)
≡ <(B)
(((a:as) ++ bs) ++ cs)Vladimir Voevodsky, Institute of Advances Studies, Princeton

Vladimir Voevodsky
A példák egy része innen származik:
Ha Haskellről/Agdráról akarsz tanulni vagy ezekkel kapcsolatos kutatásokba bekapcsolódni, ajánlom a következő (angol nyelvű) nyári iskolákat:
Érdemes még feliratkozni a Haskell-Announce levelező listára, ahol hasonló alkalmakról naprakész értesítést kapsz.